Ratio test

In mathematics, the ratio test is a test (or "criterion") for the convergence of a series

$\sum _{n=1}^{\infty }a_{n},$

where each term is a real or complex number and a_n is nonzero when n is large. The test was first published by Jean le Rond d'Alembert and is sometimes known as d'Alembert's ratio test or as the Cauchy ratio test.

The test

Decision diagram for the ratio test

The usual form of the test makes use of the limit

$L=\lim _{n\to \infty }\left|{\frac {a_{n+1}}{a_{n}}}\right|.$ 1

The ratio test states that:

• if L < 1 then the series converges absolutely;
• if L > 1 then the series diverges;
• if L = 1 or the limit fails to exist, then the test is inconclusive, because there exist both convergent and divergent series that satisfy this case.

It is possible to make the ratio test applicable to certain cases where the limit L fails to exist, if limit superior and limit inferior are used. The test criteria can also be refined so that the test is sometimes conclusive even when L = 1. More specifically, let

$R=\lim \sup \left|{\frac {a_{n+1}}{a_{n}}}\right|$

$r=\lim \inf \left|{\frac {a_{n+1}}{a_{n}}}\right|$.

Then the ratio test states that:

• if R < 1, the series converges absolutely;
• if r > 1, the series diverges; or equivalently if $\left|{\frac {a_{n+1}}{a_{n}}}\right|>1$ for all large n (regardless of the value of r), the series also diverges; this is because $|a_{n}|$ is nonzero and increasing and hence a_n does not approach zero;
• the test is otherwise inconclusive.

If the limit L in (1) exists, we must have L = R = r. So the original ratio test is a weaker version of the refined one.

Examples

Convergent because L < 1

Consider the series

$\sum _{n=1}^{\infty }{\frac {n}{e^{n}}}$

Applying the ratio test, one computes the limit

$L=\lim _{n\to \infty }\left|{\frac {a_{n+1}}{a_{n}}}\right|=\lim _{n\to \infty }\left|{\frac {\frac {n+1}{e^{n+1}}}{\frac {n}{e^{n}}}}\right|={\frac {1}{e}}<1.$

Since this limit is less than 1, the series converges.

Divergent because L > 1

Consider the series

$\sum _{n=1}^{\infty }{\frac {e^{n}}{n}}.$

Putting this into the ratio test:

$L=\lim _{n\to \infty }\left|{\frac {a_{n+1}}{a_{n}}}\right|=\lim _{n\to \infty }\left|{\frac {\frac {e^{n+1}}{n+1}}{\frac {e^{n}}{n}}}\right|=e>1.$

Thus the series diverges.

Inconclusive because L = 1

Consider the three series

$\sum _{n=1}^{\infty }1,$

$\sum _{n=1}^{\infty }{\frac {1}{n^{2}}},$

$\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}.$

The first series (1 + 1 + 1 + 1 + ⋯) diverges, the second (the one central to the Basel problem) converges absolutely and the third (the alternating harmonic series) converges conditionally. However, the term-by-term magnitude ratios $\left|{\frac {a_{n+1}}{a_{n}}}\right|$ of the three series are $1,$   ${\frac {n^{2}}{(n+1)^{2}}}$    and   ${\frac {n}{n+1}}$. So, in all three, the limit $\lim _{n\to \infty }\left|{\frac {a_{n+1}}{a_{n}}}\right|$ is equal to 1. This illustrates that when L = 1, the series may converge or diverge: the ratio test is inconclusive. In such cases, more refined tests are required to determine convergence or divergence.

Proof

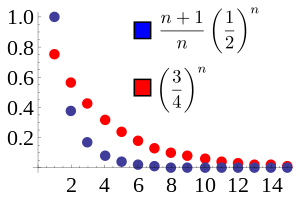
In this example, the ratio of adjacent terms in the blue sequence converges to L=1/2. We choose r = (L+1)/2 = 3/4. Then the blue sequence is dominated by the red sequence r^k for all n ≥ 2. The red sequence converges, so the blue sequence does as well.

Below is a proof of the validity of the generalized ratio test.

Suppose that $r=\liminf _{n\to \infty }\left|{\frac {a_{n+1}}{a_{n}}}\right|>1$. We also suppose that $(a_{n})$ has infinite non-zero members, otherwise the series is just a finite sum hence it converges. Then there exists some $\ell \in (1;r)$ such that there exists a natural number $n_{0}\geq 2$ satisfying $a_{n_{0}}\neq 0$ and $\left|{\frac {a_{n+1}}{a_{n}}}\right|>\ell$ for all $n\geq n_{0}$, because if no such $\ell$ exists then there exists arbitrarily large $n$ satisfying $\left|{\frac {a_{n+1}}{a_{n}}}\right|<\ell$ for every $\ell \in (1;r)$, then we can find a subsequence $\left(a_{n_{k}}\right)_{k=1}^{\infty }$ satisfying $\limsup _{n\to \infty }\left|{\frac {a_{n_{k}+1}}{a_{n_{k}}}}\right|\leq \ell <r$, but this contradicts the fact that $r$ is the limit inferior of $\left|{\frac {a_{n+1}}{a_{n}}}\right|$ as $n\to \infty$, implying the existence of $\ell$. Then we notice that for $n\geq n_{0}+1$, $|a_{n}|>\ell |a_{n-1}|>\ell ^{2}|a_{n-2}|>...>\ell ^{n-n_{0}}\left|a_{n_{0}}\right|$. Notice that $\ell >1$ so $\ell ^{n}\to \infty$ as $n\to \infty$ and $\left|a_{n_{0}}\right|>0$, this implies $(a_{n})$ diverges so the series $\sum _{n=1}^{\infty }a_{n}$ diverges by the n-th term test.
Now suppose $R=\limsup _{n\to \infty }\left|{\frac {a_{n+1}}{a_{n}}}\right|<1$. Similar to the above case, we may find a natural number $n_{1}$ and a $c\in (R;1)$ such that $|a_{n}|\leq c^{n-n_{1}}\left|a_{n_{1}}\right|$ for $n\geq n_{1}$. Then $$\sum _{n=1}^{\infty }|a_{n}|=\sum _{k=1}^{n_{1}-1}|a_{k}|+\sum _{n=n_{1}}^{\infty }|a_{n}|\leq \sum _{k=1}^{n_{1}-1}|a_{k}|+\sum _{n=n_{1}}^{\infty }c^{n-n_{1}}|a_{n_{1}}|=\sum _{k=1}^{n_{1}-1}|a_{k}|+\left|a_{n_{1}}\right|\sum _{n=0}^{\infty }c^{n}.$$ The series $\sum _{n=0}^{\infty }c^{n}$ is the geometric series with common ratio $c\in (0;1)$, hence $\sum _{n=0}^{\infty }c^{n}={\frac {1}{1-c}}$ which is finite. The sum $\sum _{k=1}^{n_{1}-1}|a_{k}|$ is a finite sum and hence it is bounded, this implies the series $\sum _{n=1}^{\infty }|a_{n}|$ converges by the monotone convergence theorem and the series $\sum _{n=1}^{\infty }a_{n}$ converges by the absolute convergence test.
When the limit $\left|{\frac {a_{n+1}}{a_{n}}}\right|$ exists and equals to $L$ then $r=R=L$, this gives the original ratio test.

Extensions for L = 1

As seen in the previous example, the ratio test may be inconclusive when the limit of the ratio is 1. Extensions to the ratio test, however, sometimes allow one to deal with this case.

In all the tests below one assumes that Σa_n is a sum with positive a_n. These tests also may be applied to any series with a finite number of negative terms. Any such series may be written as:

$\sum _{n=1}^{\infty }a_{n}=\sum _{n=1}^{N}a_{n}+\sum _{n=N+1}^{\infty }a_{n}$

where a_N is the highest-indexed negative term. The first expression on the right is a partial sum which will be finite, and so the convergence of the entire series will be determined by the convergence properties of the second expression on the right, which may be re-indexed to form a series of all positive terms beginning at n=1.

Each test defines a test parameter (ρ_n) which specifies the behavior of that parameter needed to establish convergence or divergence. For each test, a weaker form of the test exists which will instead place restrictions upon lim_n->∞ρ_n.

All of the tests have regions in which they fail to describe the convergence properties of Σa_n. In fact, no convergence test can fully describe the convergence properties of the series. This is because if Σa_n is convergent, a second convergent series Σb_n can be found which converges more slowly: i.e., it has the property that lim_n->∞ (b_n/a_n) = ∞. Furthermore, if Σa_n is divergent, a second divergent series Σb_n can be found which diverges more slowly: i.e., it has the property that lim_n->∞ (b_n/a_n) = 0. Convergence tests essentially use the comparison test on some particular family of a_n, and fail for sequences which converge or diverge more slowly.

De Morgan hierarchy

Augustus De Morgan proposed a hierarchy of ratio-type tests

The ratio test parameters ($\rho _{n}$) below all generally involve terms of the form $D_{n}a_{n}/a_{n+1}-D_{n+1}$. This term may be multiplied by $a_{n+1}/a_{n}$ to yield $D_{n}-D_{n+1}a_{n+1}/a_{n}$. This term can replace the former term in the definition of the test parameters and the conclusions drawn will remain the same. Accordingly, there will be no distinction drawn between references which use one or the other form of the test parameter.

1. d'Alembert's ratio test

The first test in the De Morgan hierarchy is the ratio test as described above.

2. Raabe's test

This extension is due to Joseph Ludwig Raabe. Define:

$\rho _{n}\equiv n\left({\frac {a_{n}}{a_{n+1}}}-1\right)$

(and some extra terms, see Ali, Blackburn, Feld, Duris (none), Duris2)

The series will:

• Converge when there exists a c>1 such that $\rho _{n}\geq c$ for all n>N.
• Diverge when $\rho _{n}\leq 1$ for all n>N.
• Otherwise, the test is inconclusive.

For the limit version, the series will:

• Converge if $\rho =\lim _{n\to \infty }\rho _{n}>1$ (this includes the case ρ = ∞)
• Diverge if $\lim _{n\to \infty }\rho _{n}<1$.
• If ρ = 1, the test is inconclusive.

When the above limit does not exist, it may be possible to use limits superior and inferior. The series will:

• Converge if $\liminf _{n\to \infty }\rho _{n}>1$
• Diverge if $\limsup _{n\rightarrow \infty }\rho _{n}<1$
• Otherwise, the test is inconclusive.

Proof of Raabe's test

Defining $\rho _{n}\equiv n\left({\frac {a_{n}}{a_{n+1}}}-1\right)$, we need not assume the limit exists; if $\limsup \rho _{n}<1$, then $\sum a_{n}$ diverges, while if $\liminf \rho _{n}>1$ the sum converges.

The proof proceeds essentially by comparison with $\sum 1/n^{R}$. Suppose first that $\limsup \rho _{n}<1$. Of course if $\limsup \rho _{n}<0$ then $a_{n+1}\geq a_{n}$ for large $n$, so the sum diverges; assume then that $0\leq \limsup \rho _{n}<1$. There exists $R<1$ such that $\rho _{n}\leq R$ for all $n\geq N$, which is to say that $a_{n}/a_{n+1}\leq \left(1+{\frac {R}{n}}\right)\leq e^{R/n}$. Thus $a_{n+1}\geq a_{n}e^{-R/n}$, which implies that $a_{n+1}\geq a_{N}e^{-R(1/N+\dots +1/n)}\geq ca_{N}e^{-R\log(n)}=ca_{N}/n^{R}$ for $n\geq N$; since $R<1$ this shows that $\sum a_{n}$ diverges.

The proof of the other half is entirely analogous, with most of the inequalities simply reversed. We need a preliminary inequality to use in place of the simple $1+t<e^{t}$ that was used above: Fix $R$ and $N$. Note that $\log \left(1+{\frac {R}{n}}\right)={\frac {R}{n}}+O\left({\frac {1}{n^{2}}}\right)$. So $\log \left(\left(1+{\frac {R}{N}}\right)\dots \left(1+{\frac {R}{n}}\right)\right)=R\left({\frac {1}{N}}+\dots +{\frac {1}{n}}\right)+O(1)=R\log(n)+O(1)$; hence $\left(1+{\frac {R}{N}}\right)\dots \left(1+{\frac {R}{n}}\right)\geq cn^{R}$.

Suppose now that $\liminf \rho _{n}>1$. Arguing as in the first paragraph, using the inequality established in the previous paragraph, we see that there exists $R>1$ such that $a_{n+1}\leq ca_{N}n^{-R}$ for $n\geq N$; since $R>1$ this shows that $\sum a_{n}$ converges.

3. Bertrand's test

This extension is due to Joseph Bertrand and Augustus De Morgan.

Defining:

$\rho _{n}\equiv n\ln n\left({\frac {a_{n}}{a_{n+1}}}-1\right)-\ln n$

Bertrand's test asserts that the series will:

• Converge when there exists a c>1 such that $\rho _{n}\geq c$ for all n>N.
• Diverge when $\rho _{n}\leq 1$ for all n>N.
• Otherwise, the test is inconclusive.

For the limit version, the series will:

• Converge if $\rho =\lim _{n\to \infty }\rho _{n}>1$ (this includes the case ρ = ∞)
• Diverge if $\lim _{n\to \infty }\rho _{n}<1$.
• If ρ = 1, the test is inconclusive.

When the above limit does not exist, it may be possible to use limits superior and inferior. The series will:

• Converge if $\liminf \rho _{n}>1$
• Diverge if $\limsup \rho _{n}<1$
• Otherwise, the test is inconclusive.

4. Extended Bertrand's test

This extension probably appeared at the first time by Margaret Martin in 1941. A short proof based on Kummer's test and without technical assumptions (such as existence of the limits, for example) was provided by Vyacheslav Abramov in 2019.

Let $K\geq 1$ be an integer, and let $\ln _{(K)}(x)$ denote the $K$th iterate of natural logarithm, i.e. $\ln _{(1)}(x)=\ln(x)$ and for any $2\leq k\leq K$, $\ln _{(k)}(x)=\ln _{(k-1)}(\ln(x))$.

Suppose that the ratio $a_{n}/a_{n+1}$, when $n$ is large, can be presented in the form

${\frac {a_{n}}{a_{n+1}}}=1+{\frac {1}{n}}+{\frac {1}{n}}\sum _{i=1}^{K-1}{\frac {1}{\prod _{k=1}^{i}\ln _{(k)}(n)}}+{\frac {\rho _{n}}{n\prod _{k=1}^{K}\ln _{(k)}(n)}},\quad K\geq 1.$

(The empty sum is assumed to be 0. With $K=1$, the test reduces to Bertrand's test.)

The value $\rho _{n}$ can be presented explicitly in the form

$\rho _{n}=n\prod _{k=1}^{K}\ln _{(k)}(n)\left({\frac {a_{n}}{a_{n+1}}}-1\right)-\sum _{j=1}^{K}\prod _{k=1}^{j}\ln _{(K-k+1)}(n).$

Extended Bertrand's test asserts that the series

• Converge when there exists a $c>1$ such that $\rho _{n}\geq c$ for all $n>N$.
• Diverge when $\rho _{n}\leq 1$ for all $n>N$.
• Otherwise, the test is inconclusive.

For the limit version, the series

• Converge if $\rho =\lim _{n\to \infty }\rho _{n}>1$ (this includes the case $\rho =\infty$)
• Diverge if $\lim _{n\to \infty }\rho _{n}<1$.
• If $\rho =1$, the test is inconclusive.

When the above limit does not exist, it may be possible to use limits superior and inferior. The series

• Converge if $\liminf \rho _{n}>1$
• Diverge if $\limsup \rho _{n}<1$
• Otherwise, the test is inconclusive.

For applications of Extended Bertrand's test see birth–death process.

5. Gauss's test

This extension is due to Carl Friedrich Gauss.

Assuming a_n > 0 and r > 1, if a bounded sequence C_n can be found such that for all n:

${\frac {a_{n}}{a_{n+1}}}=1+{\frac {\rho }{n}}+{\frac {C_{n}}{n^{r}}}$

then the series will:

• Converge if $\rho >1$
• Diverge if $\rho \leq 1$

6. Kummer's test

This extension is due to Ernst Kummer.

Let ζ_n be an auxiliary sequence of positive constants. Define

$\rho _{n}\equiv \left(\zeta _{n}{\frac {a_{n}}{a_{n+1}}}-\zeta _{n+1}\right)$

Kummer's test states that the series will:

• Converge if there exists a $c>0$ such that $\rho _{n}\geq c$ for all n>N. (Note this is not the same as saying $\rho _{n}>0$)
• Diverge if $\rho _{n}\leq 0$ for all n>N and $\sum _{n=1}^{\infty }1/\zeta _{n}$ diverges.

For the limit version, the series will:

• Converge if $\lim _{n\to \infty }\rho _{n}>0$ (this includes the case ρ = ∞)
• Diverge if $\lim _{n\to \infty }\rho _{n}<0$ and $\sum _{n=1}^{\infty }1/\zeta _{n}$ diverges.
• Otherwise the test is inconclusive

When the above limit does not exist, it may be possible to use limits superior and inferior. The series will

• Converge if $\liminf _{n\to \infty }\rho _{n}>0$
• Diverge if $\limsup _{n\to \infty }\rho _{n}<0$ and $\sum 1/\zeta _{n}$ diverges.

Special cases

All of the tests in De Morgan's hierarchy except Gauss's test can easily be seen as special cases of Kummer's test:

• For the ratio test, let ζ_n=1. Then:

$\rho _{\text{Kummer}}=\left({\frac {a_{n}}{a_{n+1}}}-1\right)=1/\rho _{\text{Ratio}}-1$

• For Raabe's test, let ζ_n=n. Then:

$\rho _{\text{Kummer}}=\left(n{\frac {a_{n}}{a_{n+1}}}-(n+1)\right)=\rho _{\text{Raabe}}-1$

• For Bertrand's test, let ζ_n=n ln(n). Then:

$\rho _{\text{Kummer}}=n\ln(n)\left({\frac {a_{n}}{a_{n+1}}}\right)-(n+1)\ln(n+1)$

Using $\ln(n+1)=\ln(n)+\ln(1+1/n)$ and approximating $\ln(1+1/n)\rightarrow 1/n$ for large n, which is negligible compared to the other terms, $\rho _{\text{Kummer}}$ may be written:

$\rho _{\text{Kummer}}=n\ln(n)\left({\frac {a_{n}}{a_{n+1}}}-1\right)-\ln(n)-1=\rho _{\text{Bertrand}}-1$

• For Extended Bertrand's test, let $\zeta _{n}=n\prod _{k=1}^{K}\ln _{(k)}(n).$ From the Taylor series expansion for large $n$ we arrive at the approximation

$\ln _{(k)}(n+1)=\ln _{(k)}(n)+{\frac {1}{n\prod _{j=1}^{k-1}\ln _{(j)}(n)}}+O\left({\frac {1}{n^{2}}}\right),$

where the empty product is assumed to be 1. Then,

$\rho _{\text{Kummer}}=n\prod _{k=1}^{K}\ln _{(k)}(n){\frac {a_{n}}{a_{n+1}}}-(n+1)\left[\prod _{k=1}^{K}\left(\ln _{(k)}(n)+{\frac {1}{n\prod _{j=1}^{k-1}\ln _{(j)}(n)}}\right)\right]+o(1)=n\prod _{k=1}^{K}\ln _{(k)}(n)\left({\frac {a_{n}}{a_{n+1}}}-1\right)-\sum _{j=1}^{K}\prod _{k=1}^{j}\ln _{(K-k+1)}(n)-1+o(1).$

Hence,

$\rho _{\text{Kummer}}=\rho _{\text{Extended Bertrand}}-1.$

Note that for these four tests, the higher they are in the De Morgan hierarchy, the more slowly the $1/\zeta _{n}$ series diverges.

Proof of Kummer's test

If $\rho _{n}>0$ then fix a positive number $0<\delta <\rho _{n}$. There exists a natural number $N$ such that for every $n>N,$

$\delta \leq \zeta _{n}{\frac {a_{n}}{a_{n+1}}}-\zeta _{n+1}.$

Since $a_{n+1}>0$, for every $n>N,$

$0\leq \delta a_{n+1}\leq \zeta _{n}a_{n}-\zeta _{n+1}a_{n+1}.$

In particular $\zeta _{n+1}a_{n+1}\leq \zeta _{n}a_{n}$ for all $n\geq N$ which means that starting from the index $N$ the sequence $\zeta _{n}a_{n}>0$ is monotonically decreasing and positive which in particular implies that it is bounded below by 0. Therefore, the limit

$\lim _{n\to \infty }\zeta _{n}a_{n}=L$ exists.

This implies that the positive telescoping series

$\sum _{n=1}^{\infty }\left(\zeta _{n}a_{n}-\zeta _{n+1}a_{n+1}\right)$ is convergent,

and since for all $n>N,$

$\delta a_{n+1}\leq \zeta _{n}a_{n}-\zeta _{n+1}a_{n+1}$

by the direct comparison test for positive series, the series $\sum _{n=1}^{\infty }\delta a_{n+1}$ is convergent.

On the other hand, if $\rho <0$, then there is an N such that $\zeta _{n}a_{n}$ is increasing for $n>N$. In particular, there exists an $\epsilon >0$ for which $\zeta _{n}a_{n}>\epsilon$ for all $n>N$, and so $\sum _{n}a_{n}=\sum _{n}{\frac {a_{n}\zeta _{n}}{\zeta _{n}}}$ diverges by comparison with $\sum _{n}{\frac {\epsilon }{\zeta _{n}}}$.

Tong's modification of Kummer's test

A new version of Kummer's test was established by Tong. See also for further discussions and new proofs. The provided modification of Kummer's theorem characterizes all positive series, and the convergence or divergence can be formulated in the form of two necessary and sufficient conditions, one for convergence and another for divergence.

• Series $\sum _{n=1}^{\infty }a_{n}$ converges if and only if there exists a positive sequence $\zeta _{n}$, $n=1,2,\dots$, such that $\zeta _{n}{\frac {a_{n}}{a_{n+1}}}-\zeta _{n+1}\geq c>0.$

• Series $\sum _{n=1}^{\infty }a_{n}$ diverges if and only if there exists a positive sequence $\zeta _{n}$, $n=1,2,\dots$, such that $\zeta _{n}{\frac {a_{n}}{a_{n+1}}}-\zeta _{n+1}\leq 0,$ and $\sum _{n=1}^{\infty }{\frac {1}{\zeta _{n}}}=\infty .$

The first of these statements can be simplified as follows:

• Series $\sum _{n=1}^{\infty }a_{n}$ converges if and only if there exists a positive sequence $\zeta _{n}$, $n=1,2,\dots$, such that $\zeta _{n}{\frac {a_{n}}{a_{n+1}}}-\zeta _{n+1}=1.$

The second statement can be simplified similarly:

• Series $\sum _{n=1}^{\infty }a_{n}$ diverges if and only if there exists a positive sequence $\zeta _{n}$, $n=1,2,\dots$, such that $\zeta _{n}{\frac {a_{n}}{a_{n+1}}}-\zeta _{n+1}=0,$ and $\sum _{n=1}^{\infty }{\frac {1}{\zeta _{n}}}=\infty .$

However, it becomes useless, since the condition $\sum _{n=1}^{\infty }{\frac {1}{\zeta _{n}}}=\infty$ in this case reduces to the original claim $\sum _{n=1}^{\infty }a_{n}=\infty .$

Frink's ratio test

Another ratio test that can be set in the framework of Kummer's theorem was presented by Orrin Frink 1948.

Suppose $a_{n}$ is a sequence in $\mathbb {C} \setminus \{0\}$,

• If $\limsup _{n\rightarrow \infty }{\Big (}{\frac {|a_{n+1}|}{|a_{n}|}}{\Big )}^{n}<{\frac {1}{e}}$, then the series $\sum _{n}a_{n}$ converges absolutely.
• If there is $N\in \mathbb {N}$ such that ${\Big (}{\frac {|a_{n+1}|}{|a_{n}|}}{\Big )}^{n}\geq {\frac {1}{e}}$ for all $n\geq N$, then $\sum _{n}|a_{n}|$ diverges.

This result reduces to a comparison of $\sum _{n}|a_{n}|$ with a power series $\sum _{n}n^{-p}$, and can be seen to be related to Raabe's test.

Ali's second ratio test

A more refined ratio test is the second ratio test: For $a_{n}>0$ define:

$L_{0}\equiv \lim _{n\rightarrow \infty }{\frac {a_{2n}}{a_{n}}}$

$L_{1}\equiv \lim _{n\rightarrow \infty }{\frac {a_{2n+1}}{a_{n}}}$

$L\equiv \max(L_{0},L_{1})$

By the second ratio test, the series will:

• Converge if $L<{\frac {1}{2}}$
• Diverge if $L>{\frac {1}{2}}$
• If $L={\frac {1}{2}}$ then the test is inconclusive.

If the above limits do not exist, it may be possible to use the limits superior and inferior. Define:

$L_{0}\equiv \limsup _{n\rightarrow \infty }{\frac {a_{2n}}{a_{n}}}$		$L_{1}\equiv \limsup _{n\rightarrow \infty }{\frac {a_{2n+1}}{a_{n}}}$
$\ell _{0}\equiv \liminf _{n\rightarrow \infty }{\frac {a_{2n}}{a_{n}}}$		$\ell _{1}\equiv \liminf _{n\rightarrow \infty }{\frac {a_{2n+1}}{a_{n}}}$
$L\equiv \max(L_{0},L_{1})$		$\ell \equiv \min(\ell _{0},\ell _{1})$

Then the series will:

• Converge if $L<{\frac {1}{2}}$
• Diverge if $\ell >{\frac {1}{2}}$
• If $\ell \leq {\frac {1}{2}}\leq L$ then the test is inconclusive.

Ali's mth ratio test

This test is a direct extension of the second ratio test. For $0\leq k\leq m-1,$ and positive $a_{n}$ define:

$L_{k}\equiv \lim _{n\rightarrow \infty }{\frac {a_{mn+k}}{a_{n}}}$

$L\equiv \max(L_{0},L_{1},\ldots ,L_{m-1})$

By the $m$th ratio test, the series will:

• Converge if $L<{\frac {1}{m}}$
• Diverge if $L>{\frac {1}{m}}$
• If $L={\frac {1}{m}}$ then the test is inconclusive.

If the above limits do not exist, it may be possible to use the limits superior and inferior. For $0\leq k\leq m-1$ define:

$L_{k}\equiv \limsup _{n\rightarrow \infty }{\frac {a_{mn+k}}{a_{n}}}$
$\ell _{k}\equiv \liminf _{n\rightarrow \infty }{\frac {a_{mn+k}}{a_{n}}}$
$L\equiv \max(L_{0},L_{1},\ldots ,L_{m-1})$		$\ell \equiv \min(\ell _{0},\ell _{1},\ldots ,\ell _{m-1})$

Then the series will:

• Converge if $L<{\frac {1}{m}}$
• Diverge if $\ell >{\frac {1}{m}}$
• If $\ell \leq {\frac {1}{m}}\leq L$, then the test is inconclusive.

Ali--Deutsche Cohen φ-ratio test

This test is an extension of the $m$th ratio test.

Assume that the sequence $a_{n}$ is a positive decreasing sequence.

Let $\varphi :\mathbb {Z} ^{+}\to \mathbb {Z} ^{+}$ be such that $\lim _{n\to \infty }{\frac {n}{\varphi (n)}}$ exists. Denote $\alpha =\lim _{n\to \infty }{\frac {n}{\varphi (n)}}$, and assume $0<\alpha <1$.

Assume also that $\lim _{n\to \infty }{\frac {a_{\varphi (n)}}{a_{n}}}=L.$

Then the series will:

• Converge if $L<\alpha$
• Diverge if $L>\alpha$
• If $L=\alpha$, then the test is inconclusive.

See also

• Root test
• Radius of convergence

References

• d'Alembert, J. (1768), Opuscules, vol. V, pp. 171–183.
• Apostol, Tom M. (1974), Mathematical analysis (2nd ed.), Addison-Wesley, ISBN 978-0-201-00288-1: §8.14.
• Knopp, Konrad (1956), Infinite Sequences and Series, New York: Dover Publications, Bibcode:1956iss..book.....K, ISBN 978-0-486-60153-3: §3.3, 5.4.
• Rudin, Walter (1976), Principles of Mathematical Analysis (3rd ed.), New York: McGraw-Hill, Inc., ISBN 978-0-07-054235-8: §3.34.
• "Bertrand criterion", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• "Gauss criterion", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• "Kummer criterion", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Watson, G. N.; Whittaker, E. T. (1963), A Course in Modern Analysis (4th ed.), Cambridge University Press, ISBN 978-0-521-58807-2: §2.36, 2.37.